JOI2018本選参加記
JOI2018本選に参加したplatypusです。最後の機会だった割にはあっさり終わった感じです。
自分の弱点(問題読めない)とか癖(部分点取れない)が改めて分かった気がするので春合宿までに全力で精進しようと思います！
以下適当な参加記です。疲れているので支離滅裂な文体ですね、あとでもっときれいにまとめるかもしれません。
day1
学校が終わる
ikasashiとBwambocosくんと一緒に学校から出る
途中でAzさんたんちゃんさん迷路さんもやし先輩と合流して昼食を食べる
つくば到着
控室で双子とWA_TLEさんなどなどガチプロかつ懐かしい面子と再会する
なんかマスコットで動植物バトルやってるところに参戦する
WA_TLEさんの足元の引っ掛かり具合がとても本家dtbっぽかった
practiceへ移動
チューターのDEGwerさんがDEGwerさんだった
practice開始
eclipseを開くも去年とソフトの挙動が違いとても焦る(今年から仮想環境配布がなくなったので去年ので練習していたのがダメだった)
スタッフさんの力を借りて何とか動かせるようになった
一通り試せたらみんな193sさんのところに集まっているので行く
emacsのゲーム怖い
そこでも動植物タワーバトルをする
色々な人を観測する
practice終了
講演会に行く
講演会が終わる
夕食会に行く
ケーキ6完する
DEGwerさんとtozangezanさんとお話をする
オオカミとのツーショットを取らせてもらう かわいい
自己紹介をする
予選で良い感じの成績取れた系のものをもらう うれしい
夕食終了
この時点でみんなのプロコン25分前
バスに乗る
移動する
バスから降りる この時点でみんプロ5分前
なんとか時間内にスタート
2完！ｗ 500点問題わからず！ｗ 爆死！ｗ
Hogetさん、双子、WA_TLEさんが高校生枠通過なのかもしれない(詳しいことはわからない)
まあ悪い記憶は早めに忘れようということで部屋に行く
風呂
熱湯だった
3問目をやるだけだといろんな人から言われて凹む
22時くらいから30分間テトリスをもやし先輩とくちもちとくらさんとやる
テトリスむずい
寝ようとする
結局緊張であまり眠れず
day2
5:40くらいに起きる
下に降りるも誰もいない
BITとdijkstraの練習をする
朝食
バス移動
眠い
バスから降りる
本選会場移動する マスコットと筆箱と水だけ持っていく
----本選競技開始----
1問目
貪欲ですね 8分でAC
2問目
えーわからず
遅延セグ木か？
いやsetで行けるか←は？
実装＋提出→WA
えー色々直すんだけどまったくWAが取れなくて焦る
去年を思い出す
まあそのあとゆっくり考えると色々おかしいことがわかる 直す
提出→TLE50点
O(NlogN)なのに低数倍きつすぎでは？
setを累積maxに直せることに気づく
提出→TLE50点
うーん、mapも消す
提出→AC(開始69分)
3問目
まあ適切に列に分解してbitDPやろなあ
実装
途中で漸化式の書き方を忘れて焦るけどまあ頑張る
提出→AC(開始111分)
まあ300点とれたので少し安心してトイレに行く
ここからの挙動は本当に最悪だった
5問目を見て5点だけ取る
4問目を見て満点解法を思いついた気になるけど、とても回りくどい方法だった(Uから近い順に頂点を追加していき、適切にDAGを更新させてVからの距離とかも考慮するとかいうよくわからない方法)
実装するもバグらせ大爆死
気づいたらもう残り15分らしいので自明な16点だけ取って終わり
----本選競技終了----
みんな360点とか405点とか422点とか430点とか取っていて、自分がいかに競プロできないかを思い知らされた
4問目はUとVをそれぞれ独立に処理してから最後に統合して考えると自明になる。本当になんで気づけなかったんだろう。
解説を聞く。みんなプロ
KMCodeさん曰く300点なら通過っぽいので少しだけ温まる でも全体10位に届いて無さそうだとわかり激冷えする
僕の予想難易度は(5,7,8,9,11)です。
セグ木に平衡二分木を載せよう!
セグメントツリーってすごいですよね！原理はシンプルでありながらも驚くほどの汎用性を持ち、 「区間の最小値」みたいな典型問題はもちろん、DPの漸化式に放り込んでみたり、結合法則が成り立つ構造体を入れてみたり、 果てには集合の簡易的な表現に使ってみたりと、競プロerの生活に欠かせないデータ構造です。 （筆者も先日のPCK予選で2回ほどお世話になりました）
今回はこのセグメントツリーと同様に有名な、でも標準ライブラリに実装されている機能で普段事足りているから実装したことがない人も多いかも？という 「平衡二分木」をセグメントツリーに載せてみたいと思います！でもその前に、少し予習をしておきましょう
プログラミングコンテストでのデータ構造
プログラミングコンテストでのデータ構造 2 ～平衡二分探索木編～
2つともiwi先生のスライドで、一つ目は後半にセグメントツリーの説明が、２つ目はまるまるtreapによる平衡二分木の実装が入っています。
上のスライドを読むのもだるい！っていう方は以下の２つのポイントだけ理解していればOKです。 （だるくなってきたので以下からセグメントツリーを「セグ木」と呼びます）
・基本的なセグ木の書き方
さすがにこれはほかの方々がすでに何回も紹介されていると思うので、このブログで取り上げるべき話題ではないと思われます。
・平衡二分木は何ができるか？
「木」と言っておきながら、平衡二分木は「常にソートされている数列」みたいに考えておくのが一番無難だと思います。 例えば、以下のすべてのクエリをO(log N)で処理できます。(N=木の大きさ)
①値の挿入(insert)・値の削除(erase)
②k番目の値の出力
③値の検索
④ある値未満の数列 と ある値以上の数列 への分割(split) ex) {1,2,4,5,7}のとき、5を境目に分割して {1,2,4} {5,7} にする
⑤ある値未満の数列 と ある値以上の数列 の統合(merge)
⑥数列内のすべての値の和、値の個数、値の最大値最小値etc...
⑤の統合(merge)についてですが、あらゆる平衡二分木を統合できるわけではないことに注意です！ 例えば、{1,2,4}{5,7}は、どの左の要素よりも右側の要素のほうが大きいので統合可能ですが、{1,2,5}{4,7}などは無理です。（もちろんerase/insertを使い、値を一つずつ引っぺがしてはもう片方に入れていくとO(N log N)で可能です） 一見あまり役に立たなさそうなmergeですが、内部実装などで使う場合があるので機能の一部に入っています。 実はC++の標準ライブラリに実装されている「std::set」および「std::map」は上記のうち①③しか実装されていません！ また、g++の拡張機能であっても上の2つに加えて②しか使えないそうです。 なので④⑤⑥(とりわけ⑥)の機能が欲しい今回のブログのテーマにおいては、平衡二分木は自前で全部実装したものを用意しておいてください。
本題１
以下の問題を考えてみましょう。
「横幅がN、縦に無限に広い長方形がある。大きさ1×1のマス目に区切られており、各マス目のコストは最初0である。 今から2種類のクエリを合計Q個処理せよ。
クエリa:(l,r,a,b,x)が与えられ、幅[l,r)、高さ[a,b)の長方形内に存在するすべてのマス目のコストにxを足す。
クエリb:(x,y)が与えられ、座標(x,y)に存在するマス目のコストを出力する。 N,Q≦10^5」
クエリa:(l,r,a,b,x)が与えられ、幅[l,r)、高さ[a,b)の長方形内に存在するすべてのマス目のコストにxを足す。
クエリb:(x,y)が与えられ、座標(x,y)に存在するマス目のコストを出力する。 N,Q≦10^5」
例： N=5の時
クエリa,(1,5,2,4,5)
クエリa,(2,6,3,5,-1)
クエリb,(0,0)→0
クエリb,(1,2)→5
クエリb,(3,3)→4
クエリb,(5,4)→-1
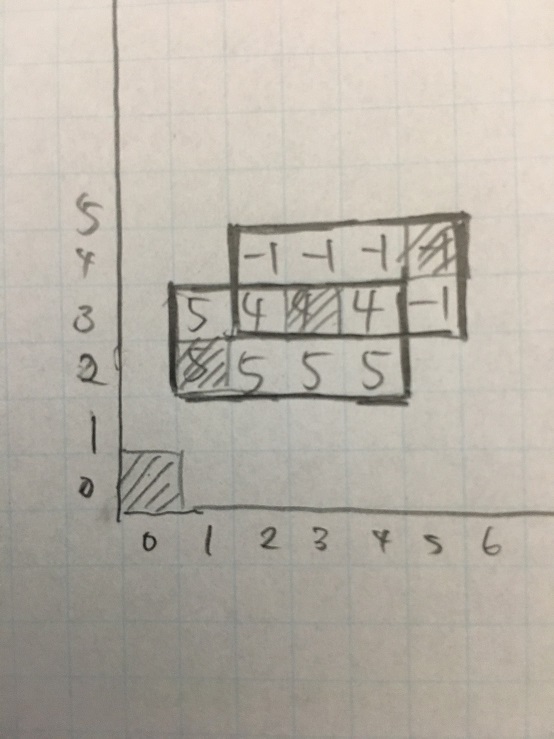
解法： セグ木のすべてのノードにpair<int,int>のような、二つの値を要素に持つ平衡二分木を載せます。 最初はすべての平衡二分木を空にします。
クエリaが来た時、
①[l,r)区間に対応するノードを通常のセグメントツリーのように列挙します。セグ木の性質により、ノードの数は高々$O(log N)$個であることがわかります。
②上のノードに対し、ひとつずつに(a,x)と(b,-x)、2つの値を挿入します。 一回の挿入にかかる計算量は$O(log Q)$ですので、全体としては$O(log N * log Q)$でクエリは処理できます。
クエリbが来た時、
①すべてのノードのうち、xを含む(区間の左端≦x≦区間の右端 が成立する)区間を列挙します。セグ木の性質により、これの個数も高々O(log N)です。
②すべてのノードの平衡二分木を見ます。それぞれの木に対し、値が(y,∞)以下の要素の和を求め、その第二値(C++で言うとpairのsecond)を足し合わせます。平衡二分木の分割・和の取得の計算量は$O(log Q)$のため、全体としては$O(log N * log Q)$で処理できます。 以上の処理で出てきた値がクエリbの答えになります。
以上のアルゴリズムを使うと、Q個のクエリに対し、$O(Q * log Q * log N)$の計算量で処理できます。 $O(N)=O(Q)$の場合、$O(N log^2 N)$となるため、愚直にやった場合の$O(N^2)$に比べて改善がされています。
証明： なぜ上のアルゴリズムによって正しい結果が得られるのでしょうか？ まず、より簡単な問題から分析していきましょう。
「無限に長い数直線がある。今から2種類のクエリを合計Q回処理せよ。
クエリa:(l,r,x)が与えられ、[l,r)の区間に一様に値xを足す。
クエリb:(k)が与えられ、数直線の場所kの値を出力する。 Q≦10^5」
クエリa:(l,r,x)が与えられ、[l,r)の区間に一様に値xを足す。
クエリb:(k)が与えられ、数直線の場所kの値を出力する。 Q≦10^5」
これはBITとクエリ先読みによる座標圧縮を使えば簡単に求まる問題です。ただ、メモリを節約するために、またinteractiveな問題にも対応するために、平衡二分木を使うこともできます。
まず、 空の平衡二分木を１個持ちます。
クエリaが来た時、(l,x)と(r,-x)、２つの値を挿入します。（計算量は$O(log N)$）
クエリbが来た時、平衡二分木中のうち、値が(k,∞)以下のすべての要素の和を求めます。この時、この第二値がクエリbの答えです。（分割と値の総和の取得で処理できるので、これも計算量は$O(log N)$） なぜならば、クエリbのkについて、すべてのクエリaの[l,r)を見たとき、 k<lならば何も足されないので0 l≦k<rの時、(l,x)は足されますが(r,-x)は足されないのでx r≦kの時(l,x)、(r,-x)が両方足されるのでx+(-x)=0 となるからです。
この性質を応用して、2次元に拡張しましょう。 二次元平面を列ごとに分割し、1列ごとを平衡二分木で管理しましょう。 幅[l,r)高さ[a,b)の長方形に一様に値xを足すときは、 l≦i<rであるすべてのiについて、 「i番目の平衡二分木に(a,x)と(b,-x)を挿入する」 という処理をすれば、各クエリはO(N log Q)で処理できそうです。
さらに、[l,r)という区間において、l≦x<rを満たす一つ一つのxを見ていくのは無駄です。 横の区間をセグ木のように持ってみましょう。次に、各区画に平衡二分木を持たせます。 こうして、クエリaが来た場合は、 区間[l,r)は[l1,r1),[l2,r2),[l3,r3),[l4,r4),...,[ls,rs)というs個の区間に分けることができます。 セグ木の性質上、sは$O(log N)$であることがわかります。 そして、これらs個の区画のそれぞれの平衡二分木に(l,x),(r,-x)を足します。 計算量は全体で$O(log N * log Q)$です。 さて、クエリbが来たときはどうすればよいでしょうか？ これについては、xを含んでいるすべての区間(l≦x<rであるような[l,r))を見ます。 セグ木の性質より、この条件を満たす区間の個数は$O(log N)$です。 そして、各区間の平衡二分木に対し、「(y,∞)以下の値の和」を求め、その総和が答えになります。
実践
データ構造はACしないと意味がない！というわけで2問ほど
NCR CodeSprint(HackerRank) Points and Fences
問題文
すこし考察をすると、この問題は「長方形区間に値をxorする」「ある点の値を取得する」 の二つのクエリを高速に処理すればよいことがわかります。
これは単にセグ木に平衡二分木を載せて、平衡二分木中のすべての値のxor値を取得する機能を追加すれば簡単に処理できます。 計算量も$O(q * log n * log q)$と十分高速です。 （実はこの問題はセグ木にBITを載せたデータ構造でも解くことが可能のようですが、こっちのほうが貼るだけ、ですよね！）
ukuku09コンテスト(Hamako Online Judge) ghoststudents2
問題文
クエリ2の[c,d]を、二次元平面上の点(c,d)とみなして考えてみましょう。 この時、クエリ1はすべて、「ある長方形範囲に1加算する」ということになります。
この長方形の範囲は、先読み＋座標圧縮や、単純な平衡二分木の操作で簡単に求まるので、 問題は$O(Q * log (10^6) * log Q)$で求めることが可能です。 なお、この問題の想定解法である$O(Q * N * log N)$の定数倍高速化よりこちらの方法のほうがはるかに簡単に解くことができますし、理論上はこちらのほうが圧倒的に速いです。
（実際は平衡二分木による定数倍がかなり重く、AVL木や赤黒木などの割柏高速なデータ構造でないとAC出来ませんでした。）
以上のように、足し算だけでなくxorのような累積可能な演算子、また一次元区間のクエリにこのデータ構造は強いことがわかります。一次元区画のクエリといえば、AtCoder Regular Contest 067のYakiniku Restaurantsもこれで解くことが(理論上)可能です。ただ、あの問題はクエリ制ではないので、imos法でも解けてしまいます。なんでもかんでもデータ構造に頼るとかえってTLEやバグの原因にもなるので注意ですね…
本題２
もう一つ問題を考えてみましょう！
「平面上に点がN個散らばっている。i個目の点の座標は(i,Y_i)であり、コストはC_iである。 今から2種類のクエリを合計Q個処理せよ。
クエリa:(x,y)が与えられ、Y_xにyを代入する
クエリb:(l,r,a)が与えられ、幅[l,r)、高さ[a,∞)の長方形内に存在する点のコストの合計を出力する N,Q≦10^5」
クエリa:(x,y)が与えられ、Y_xにyを代入する
クエリb:(l,r,a)が与えられ、幅[l,r)、高さ[a,∞)の長方形内に存在する点のコストの合計を出力する N,Q≦10^5」
例：
N=6 Y={1,1,4,5,1,4} C={8,10,1,9,1,9}
クエリb,(3,8,3,7)→1+9+9=19
クエリa,(5,5)
クエリa,(3,2)
クエリa,(6,7)
クエリb,(3,8,3,7)→9+1=10
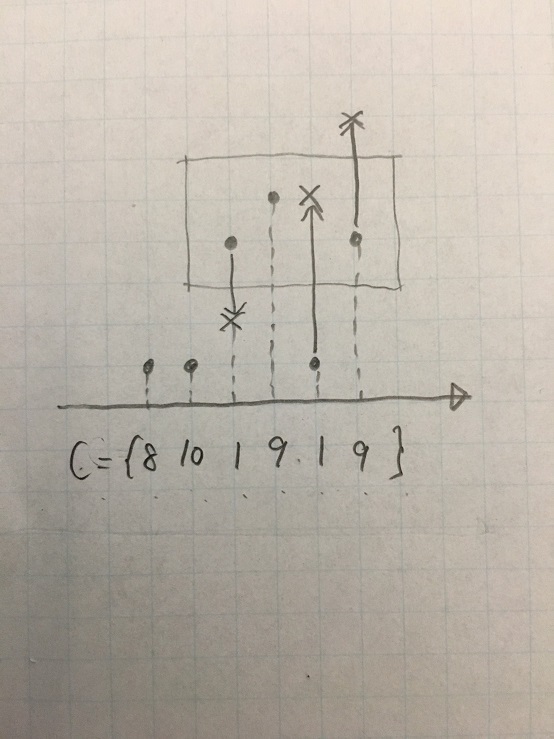
解法： セグ木にpair<int,int>などの２つの値をもつ平衡二分木を持たせます。 次に、各iについて、[i,i+1)の区間に対応するノードに(Y_i,C_i)を代入します。 また、各区間[l,r)の平衡二分木に、その二つの子[l,m)と[m,r)の平衡二分木の全要素を入れます。 すると、図のようになります。(蟻本の「領域木」参照)
空間計算量は$O(N log N)$です。また、構築にかかる時間計算量は$O(N log^2 N)$であり、すこし操作を加える(マージソート的なテクニックを使う)と$O(N log N)$に落とせます。ただ、$log N$が一つ減るだけですので、コストパフォーマンス的におすすめは余りしません。
クエリaはxにかぶるすべての区間(l≦x<rであるような区間[l,r))について、平衡二分木からY_iを削除し、xを挿入します。計算量はO(log^2 N)です。
また、クエリbは[l,r)を[l1,r1),[l2,r2),[l3,r3),[l4,r4),...,[ls,rs)というs個の区間に分け、それぞれの区間の平衡二分木について、値がa以上の全要素の和を取得し、その第二値の総和を出力すればよいです。 この処理は、ちょうど本題１で説明したアルゴリズムと逆のことをやっています。即ち、 区間更新一点取得か一点更新区間取得か、ということです。 以上のアルゴリズムを使うと、Q個のクエリに対し、$O(Q * log^2 N)$の計算量で処理できます。 $O(N) = O(Q)$の場合$、O(N log^2 N)$となるため、愚直にやった場合の$O(N^2)$に比べて改善がされています。
証明： アルゴリズムの正当性はほぼすべて本題１と被るので割愛いたします。 こちらのほうが区間に対する平衡二分木の取り方がシンプルなので、直感的かもしれません。
実践：
Codeforces Round #433 Div1C Boredom
問題文
すこし考察するとまんま「本題２」の問題であることがわかります。 座標圧縮すらする必要もなく、$O(N log^2 N)$で投げるだけです。 （なお、wavelet matrixというさらに怖いデータ構造でも殴れるらしいです）
Codeforces Round #431 Div1C Goodbye Souvenir
問題文
この問題は、b_i = (同じshapeである最も近くにある左の図形の位置)とすると、 二番目のクエリは「l≦i≦r∧b_i≧lを満たすすべてのi-b_iの和」となります。 これは、すべての1≦i≦Nについて、位置(i,b_i)、コスト(i-b_i)の点があるとき、 幅[l,r)、高さ[l,∞)の長方形内に存在する点のコストの合計であることがわかります。 よって、この問題もセグ木に平衡二分木を載せることによって解くことが可能です。 (この問題はクエリ先読みが可能なので、セグ木にBITを載せることでも解くことができます)
このように、こっちのデータ構造も一次元区間のクエリにある程度強いことがわかります。 領域木の上位互換であり、かつ実装も(平衡二分木がすでに手元にあるならば)意外と単純なので、こっちも使ってみてはいかがでしょうか？
まとめ
以上はセグ木に平衡二分木を載せると何ができるかの紹介でした！
確かにライブラリ持ち込み不可の環境では文字数の多さや実装量の多さから余りお勧めはできないかもしれませんが、手元に置いておくといざというときに「貼るだけ」を体現できるようになるはずです！また、領域木やBITを持つセグ木よりも先読みをしなくてよく、煩雑な処理を挟まなくてもよいことが魅力だと思います。みんなも平衡二分木とセグ木を組み合わせて、さらに充実した競プロライフを楽しんでください！
あとでソース貼るかも！
PCK2017予選記事
PCKお疲れさまでした！
結果からいいますと、僕たちのチームは9完1WAでした。あとでも言いますが、この1WAは集中していれば絶対生やさなかったWAなのでとても悔しいです…
わが校のコンピューター部の高校部長である相方は非競プロerなので、どうなのかなーと心配していたのですが、supercon同様、詰まったときに頭を初期化というか、別の方針に切り替えさせてくれる役目を果たしてくれました。あと何よりバグが少ない！1~5をほぼほぼ書き直さずに提出していたのは正直僕より強いなあと思いました。
文化祭前の大事な時期なのにチームを組んでくれた相方に感謝！
では当日の流れを箇条書きに
・緊張で5:45くらいに起きる。流れでスマホをいじる←よくない
・学校に行って、wi-fiを特別に接続してもらうためにパソコンを渡す
・HR中LISのdpを蟻本で復習する
・牛ゲーって何だろう→初めて知る、緊張する
・まずい、緊張してまったく授業が聞こえない
・授業終わった！この時点でPCK開始45分前
・プリンターを部室から回収する。
・なんとプリンターからSurfaceにつなぐUSBケーブルがないことがわかり、とても焦る
・なんか先生がうまい具合にやってくれることを祈りつつ飯
・食い終わったらもう開始15分前
・相方が会場に来ない
・5分前でようやく相方到着。ここでプリンターの紙がないことに気づき急いで部室からとってくる
・開始30秒くらい前に戻ってくる、開始とほぼ同時に紙をセット
・6問目プリントアウトしてもらう。
・1問目を早速相方がAC
・7問目をプリントアウトしてもらう。
・7はぱっと見bitDP？こんなめんどい問題出すか？
・6に手こずる→セグ木でえいしよ！(は？)
・2問目を相方がAC
・8問目をプリントアウトしてもらう
・ん？簡単じゃね？
・↑これは罠で、難しい
・8わからんぞ
・3問目を相方がAC
・9問目をプリントアウトしてもらう
・ほほお(面白い問題)
・とりあえず貪欲はわかる
・どうせ平衡二分木か何か使うんか？
・わからずひるどでちょっと焦る
・4問目を相方がAC←ここまで0WA、相方有能
・10問目をプリントアウトしてもらう
・でも5問目も少し見るか
・相方と相談してgcdとかでもにょれば良いとわかる
・ペアプロする。小学生の入試問題でもでたなあ、そういえば
・まあこれもAC
・相方が6問目読んでる間に実装する
・セグ木の中身をintにしたせいで手元WAをする、15分ほど浪費する
・申し訳なさでいっぱいの中提出→AC
・ここで順位表の存在に気づく
・見るとなんか10位いないっぽい
・7問目の貪欲を相方が提唱する。でもこれは嘘だった。
・結局bitDPでやる。コピー&ペーストを5行×18回やった怖いコードを書く
・うーん、手元で合わない
・焦る(bitDP許さん)
・20分かけて問題文のHとNを読み間違えていたことが判明
・許さないという強い意志の元提出→AC
・順位表見るとまだ10位以内
・焦るな…焦るな…
・8と9を考える
・8の貪欲を相方が提唱する。でもなんか僕の競プロ的センサー（笑）ではそれは嘘っぽいって言っておく
・8問目、二分探索＋尺取りでできるか！？
・できそうだけど、尺取りは絶対バグるので二分探索に変換する
・実装し終わる→手元でWA
・なんと20分かけて、それは1145148101919をintにぶち込んでいたせいだと判明
・正直死にたくなった(もっと強く生きろ)
・AC←この時点で終了まで40分
・ここで順位表を見ながら一休憩
・俺たちもし9完で0WAだったら2位になるんじゃね！？とか言う。
・10問目を考える
・強連結をつぶして、あとは残ったDAGに適切に辺を張りたい…みたいなことを相方に説明する
・↑一番長いパスを貪欲につぶせば？と相方が言う。でもなんか僕の競プロ的センサー（笑）ではそれは嘘っぽいって言っておく
・↑この僕の発言は大嘘で、実は相方が正しかった(せっかくの正しい考察を強連結のごとくつぶした僕は害悪では？)
・9問目に移行
・平衡二分木+BITを使うとこういうことになる、みたいなことを相方に説明するが、これコストオーバーしないような奴を高速に選ぶのはどうしようかな…とかぼやく
・相方が「それ区間上じゃね？」と天啓を授かる
・↑はい自明セグ木、相方は競プロの才能があるのでは！？
・とりあえず興奮しながら実装
・順位表凍結される→この時点で6位
・なんか事前に用意していたBITが閉区間なのにseg木は半開区間で実装していたせいで僕の頭こわれる
・混乱している中コードを書き上げた→手元では通る…
・①もうちょっとコードを吟味する ②やけくそで提出する
・相方は中立だったが僕は②を推したため(大馬鹿)提出する
・9問目WA_WA_WA_WA_...
・思わず叫んだ
・もう一度コードをにらむと、案の定閉区間であるものを半開区間にしたりしている
・ちゃんと考察して直す
・提出→やっとAC
・この時点で終了10分前なので試合を放棄する
・11問目もついでに見ておく→まったく理解できない ってなる
・先生と雑談する
・競技終了
・9完1WAなら5位以下だなとか言う。
・先生が僕たちに啓発(?)されてVSを入れたらしい→これは競プロをするしかないな、数学科教員だし！→宗教勧誘の断られ方と同じような感じでやんわりと断られた
・相方と雑談、そこそこ幸福なひと時を過ごして終わる。
まあこの後用事などでTwitterに浮上できなかったのですが、何より相方すごいです！
9問目とか、8問目のデバッグとかで救われました！
あと、凍結時2位のsolarsとか4位のdisprogramとかはすごーく速く解いていて、地力の差を見せつけられた感じですね…
何より僕がエンバグをしすぎているというのがありました…本選またはもう一つの本選までに実装力も鍛えなきゃなあと感じました。
まだ順位や通過の可否などはわかりませんが、結果が出たらまた追記しようと思います。
Codeforces AIM Tech Round Div1C Centroids
概要
$N$個の頂点で構成された無向木が与えられる。 あなたは最大で一回、辺を削除し別の頂点と頂点を辺で結びなおすことができる。
ただし、辺を追加した結果も木でなければいけない。
この時、適切な操作を行い$i$番目の頂点を重心にすることはできるかを判定しなさい。
重心とは？
重心とは、削除して1つ以上の木に分解したとき、 それらの木のどれもが頂点数$n/2$を超えないような頂点のことである。
木の「中心」との違いに注意せよ。また、重心が複数個ある可能性にも留意せよ。
制約
$2\le N \le 4*10^5$
考察
まずは各頂点に対し、重心かどうかの判定をしよう。 これは簡単な全方位木dpで求まるため、ここでは扱わない。
次に、すでに重心である頂点は自明に(0回操作することによって)重心にすることができるので、 重心でない頂点を考える。
重心でない頂点を削除すると、定義より、$n/2$を超える大きさの連結成分ができる。
このような$n/2$を超える大きさの連結成分は一個しかないので、この連結成分をどうにかして操作することによって 2つの$n/2$以下の連結成分に分解できないかを考える。
まず、適当な重心を根として、木を再構成する。
そうすると、$n/2$を超える大きさの連結成分は必ずどの頂点の親側にあることがわかる。
根を通らずに連結な頂点をグループ分けすると、 どのグループの大きさも$n/2$を超えないので、 自分が含まれているグループ以外のグループの中で一番大きいグループと、そうでない頂点で分割するのが一番良い。(下の図を参照)
ただ、一つだけ例外があり、自分のグループのサイズがちょうど$n/2$の場合、自分以外の全グループに加え、根自体もまとめて分割するのがよい。(下の図を参照)
いずれにせよ、分割によって無事大きさn/2以下の二つの連結成分に分解できればOK、そうでなければその頂点は重心になれない。
木の問題、難しい
Codeforces Beta #84 Div1C Lucky Tree
概要
$N$頂点で構成された無向木が与えられる。 無向木の各辺には"Lucky"かそうでないかの属性がついている。 頂点から頂点までのパスにLuckyな辺が一つ以上含まれている時、それをLuckyなパスと呼ぶ。 異なる頂点$i,j,k$について、$i$から$j$までのパスと$i$から$k$までのパスが共にLuckyである$(i,j,k)$の通り数を求めよ。
制約
$1\le N\le 10^5$
考察
iを全頂点について試す。この時、$i$からLuckyなパスでつながっている頂点の数を$A(i)$とすると、 $A(i)*(A(i)-1)$が$(i,j,k)$の通り数となる。
$A(i)$をどう求めればよいだろうか？ 一見辺$e(u→v)$について、$e$を通らずに$v$と連結なすべての頂点の集合についてDPすればよさそうである。
しかしもし頂点の出次数が非常に大きい場合(例えばウニグラフの場合)計算量は$O(N^2)$となり、間に合わない。 (virtual中はこれを$O(N)$と勘違いしてしまいTLEした。)
そこで、「全方位木DP」と呼ばれるテクニックを使おう。
全方位木DPとは、まず単純な木DP(各頂点を親とした部分木についてのDP)を行い、その計算結果をもとに今度は各頂点を根とした木全体についてのDPをすることである。
まず適当な頂点$par$を根にして有向な木にしよう。 次に、$F(i):=i$を親とした部分木について、$i$からLuckyなパスでつながっている頂点の個数を算出しよう。
これは各$i$の子$j$について、$i$と$j$をつなぐ辺がLuckyな場合$C(j)$、そうでない場合$F(j)$の総和を求めればよい。
(ただし、$C(x)$とは、頂点$x$を親とした部分木の頂点の個数である。)
これは単なる木DPである。
今度は、$G(i):=i$を親とした部分木に含まれない頂点について、$i$からLuckyなパスでつながっている頂点の個数を算出したい。
$i$が$par$の場合、当然$G(i)=0$である。
そうでない場合、$i$の親$j$について、 $i$と$j$をつなぐ辺がLuckyな場合$C(par)-C(i)$、 そうでない場合、$G(j)+F(j)-F(i)$である。
理由は下の図を参考にしていただきたい。
後は、$A(i)=F(i)+G(i)$なので、一番最初に考察した式によって答えを算出すればよい。
手書き図見にくいな(だったらつくるな)
Codeforces #150 Div1B/Div2D Hydra
問題要約：
頂点u-vをつなぐ辺を一つ持ち、端点の片方がuの辺をh個、端点の片方がvの辺をt個持つグラフをHydraグラフと呼ぶ。(図参照) 頂点数n,mのグラフGと整数h,tが与えられるとき、Gの部分グラフにHydraグラフが含まれるか？
制約：
\(n,m\le 10^5\)
\(h,t\le 100\)(超重要)
解法：
Hydraグラフのu-vをつなぐ辺を全通り試そう。u-vを固定すると、注目する頂点は以下の3つに分類できる。
①uと隣接している頂点
②vと隣接している頂点
③u,v両方と隣接している頂点
図にすると、このように分類できる。
（ただし、③に含まれるものは①、②から除外する）
頂点xの次数を\(deg(x)\)で表す。この時、①②③の個数をそれぞれ\(P,Q,R\)とすると、
\(P+Q+R=deg(u)+deg(v)\)である。
また、Hydraグラフを作ることができる必要十分条件は
\(P+p\le h,Q+q\le t,p+q\le R\) である。
P,Q,Rを求めることは簡単ではなさそうだ。ここでは前処理により簡単に求められる\(deg(u)\)と\(deg(v)\)からHydraグラフの有無を検出しよう。
A.\(deg(u)\lt h+1\)または\(deg(v)\lt t+1\)の時、
そもそも辺が足りない。当然ながらHydraグラフは作れない。
B.\(deg(u)\le h+t+1\)かつ\(deg(v)\le h+t+1\)の時、
たとえ全ての頂点が③であっても、また逆に③の頂点が一つもない場合でも、Hydraグラフを構築できる。
C.その他
この場合は素直に\(P,Q,R\)を求めよう。ここで\(h,t\le 100\)と小さいことを活用できる。
AでもBでもないので、\(h+1\le deg(u)\lt h+t+1\)かつ\(t+1\le deg(v)\lt h+t+1\)である。つまり、頂点u,vに隣接する頂点を全列挙しても\(deg(u)+deg(v)=\)高々\(2(h+t+1)\)個であり、計算量は全体で見ても\(O(m(h+t))\)と十分小さい。
以上のA,B,Cの場合分けは以下のように図示できる。
h,tの制約を見落としていてvirtual中は解けなかった。
SRM n周目(n > 1)
なんか1か月半ほど前にSRM6xxのDiv1 Easyで解けるものを全部解くといいましたが、やっと3日ほど前に1周することができました。
やはり難易度にはとてもばらつきがあったので、問題をこなすスピードは結構変動しました。中にはただの実装ゲーというべき余り良問でないものも存在しましたが、最終的に100問中68問解くことができました。(1回以上system testing failedしたものも含めます)
Div1 Easyの難しめの問題のサンプルとして、解けなかった残りの32問のSRM番号を貼り付けておきます。青コーダーくらいの人ならどれもじっくりと考察しなければいけない問題だと思うので、2,3問やってみてはいかがでしょうか。
602,603,607,608,614,616,622,629,630,631,633,638,639,642,645,646,653,654,659,662,665,666,669,672,677,681,682,683,686,692,697
ではでは
(追記：616はあまりにもやるだけな問題だったので飛ばした問題でした。考察要素は全くないので一覧から消しました。)
2周目、つらい
